Bounding Portfolio Risk with Incomplete Covariance Information

SDP > Conic problems | LMIs | Standard Forms | Applications > Portfolio Risk | Next

Portfolio variance
Variance with complete covariance information
Bounding variance with incomplete covariance information

Portfolio Variance

Consider (see here for more background) a portfolio of

assets, which is described by a vector $x in mathbf{R}^n$ , with x_i

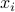the amount (in, say, US dollars) invested in the

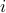-th asset. We are interested in defining, and quantifying the risk associated with holding the position (as described by

) over a certain time period into the future.

We can define the vector 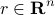$r in mbox{bf R}^n$ , with r_i

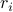the rate of return of the

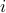-th asset at the end of the period considered. The return of the portfolio is y = r^Tx

Of course,

is unknown. Let us model this uncertainty by assuming that

is a random variable. Then, the return y=r^Tx

is also a random variable. We define the risk of the portfolio

, and denote by sigma^2(x)

, the variance of its return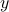

. That is:

where

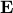is the expected value of the portfolio's return, and mathbf{E}

denotes the expectation operator with respect to the distribution of the random variable

Evaluating the risk is useful to compare different portfolios. Some might have a higher expected return than others; this usually comes at the expense of higher values of risk. The risk defined above suffers from several practical limitations, and we explore one of them here.

Complete Covariance Information

With

, and

not random (we just take a position at the beginning of the investment period, and hold it until the end), we have

$sigma_{Sigma}^2(x) := mathbf{E} ( y - hat{y})^2 = mathbf{E} left((r - hat{r})^Txright)^2 = x^T Sigma x,$

where $Sigma:= mathbf{E}(r-hat{r})(r-hat{r})^T$ is the covariance matrix of the vector of returns.

If this matrix is known, the risk (as we defined it) is easily computed via the matrix-vector product. However, in practice, the covariance matrix is hard to estimate precisely.

Bounding Risk with Incomplete Covariance Information

Assume now that the covariance matrix is only partially specified. For example, in a case with n=3

assets, we might describe our uncertainty as

where the symbol

denotes that we believe that the corresponding assets (in this case, assets

and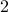

) are positively correlated, while

denotes negative correlation. Here, the symbol “

” denotes complete uncertainty on the sign of the correlation. The above covariance information is only partial, with only the diagonal elements (variance of each asset) given hard numbers. Denote by mathbf{Sigma}

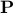the set of symmetric matrices that satisfy the above pattern. This set is a polytope, which we will denote mathbf{P}

, in the space 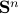$mathbf{S}^n$ of symmetric matrices, since it is defined as the following ordinary inequalities:

$mathbf{P} := left{ Sigma = Sigma^T in mathbf{R}^{3 times 3} ~:~ begin{array}[t]{l} Sigma_{11} = 0.1, ;; Sigma_{22} = 0.3, ;; Sigma_{33} = 0.6, Sigma_{12} ge 0, ;; Sigma_{13} le 0 end{array} right} .$

Of course, any symmetric matrix in the set 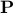mathbf{P}

is not necessarily a covariance matrix. In order for it to be a covariance matrix, it has to be positive semi-definite.

We define the worst-case risk as the largest variance of the portfolio that can be attained by some covariance matrix:

$max_{Sigma} : sigma_{Sigma}^2(x) ~:~ Sigma in mathbf{P}, ;; Sigma succeq 0.$

The above is an SDP in (matrix) variable 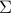Sigma

. It is implementable in CVX as follows.

CVX syntax

vars = [0.1; 0.03; 0.6]; % given asset variances
cvx_begin
    variable S(n,n) symmetric
    maximize( x'*S*x )
    subject to
        diag(S) == vars;
        S(1,2) >= 0;
        S(1,3) <= 0;
        S == semidefinite(n);
cvx_end

Consider for example the case when the portfolio is given by the vector x = (0.1, 0.5, 0.4)

. The maximum portfolio variance is $sigma_{rm max}^2 = 0.1584$ . We can compare this number with the best (that is, smallest) portfolio achievable. Replacing the maximization by minimization (which is permitted in SDP, as the objective is linear), we obtain the most optimistic value of $sigma_{rm min}^2 = 0.0367$ . Thus, under our uncertainty model for the covariance, the portfolio variance can change in relative amount by the staggering amount of

$frac{sigma_{rm max}^2 - sigma_{rm min}^2}{sigma_{rm max}^2} approx 70 % .$