Robust Stability of Linear Dynamical Systems
Motivation
Lyapunov stability criterion
Robust stability
Robust linear control
Motivation
The time-behavior of many dynamical systems can be well modeled using a linear system of the form

where  is the state, which encapsulates the state of the system at time
is the state, which encapsulates the state of the system at time 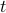 ,
,  contains control variables, and
contains control variables, and  are matrices of appropriate size.
(For more details, see here.) When
are matrices of appropriate size.
(For more details, see here.) When  are constant, we say that the system is time-invariant.
are constant, we say that the system is time-invariant.
A continuous-time version of the above takes the form

We focus on these continuous-time models here.
A crucial problem in dynamical systems is asymptotic stability. Roughly speaking, we would like to know if, irrespective of the initial condition  , and when there are no inputs (
, and when there are no inputs ( for every
for every 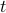 ), then
), then  when
when  . If not, we would like to see how to act on the system with certain inputs that are functions of the state, so that the resulting system becomes stable.
. If not, we would like to see how to act on the system with certain inputs that are functions of the state, so that the resulting system becomes stable.
Lyapunov stability criterion
Lyapunov invented (circa 1890) a method that provides a (in general, only sufficient) condition for asymptotic stability. Assume that there is a positive-definite function of the state,  that decreases strictly along every trajectory. Then
that decreases strictly along every trajectory. Then  converges to zero as
converges to zero as  . The physical interpretation of
. The physical interpretation of 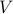 is that it acts as a total energy for the system. For mechanical systems,
is that it acts as a total energy for the system. For mechanical systems, 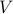 can be chosen to contain the kinetic and potential energy.
can be chosen to contain the kinetic and potential energy.
When  , and with
, and with  , we have
, we have

Thus a sufficient condition for stability is  on any trajectory. Expressing this condition for
on any trajectory. Expressing this condition for 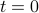 and for arbitrary
and for arbitrary  results in the following sufficient condition for asymptotic stability.
results in the following sufficient condition for asymptotic stability.
Lyapunov's sufficient condition for asymptotic stability: there exist  such that
such that
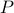 is positive definite;
is positive definite;for every
 ,
,  is negative definite.
is negative definite.
It turns out that for time-invariant systems ( independent of
independent of 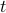 ), the above is also necessary.
), the above is also necessary.
Robust stability
Now assume that  is not completely known, say it can take its values arbitrarily in a finite set
is not completely known, say it can take its values arbitrarily in a finite set  . The matrices
. The matrices  can represent the behavior of the system under different operating conditions, and allow to model the uncertainty about the model's parameters. Based on Lyapunov's condition above, the following condition guarantees stability irrespective of the choice of
can represent the behavior of the system under different operating conditions, and allow to model the uncertainty about the model's parameters. Based on Lyapunov's condition above, the following condition guarantees stability irrespective of the choice of  in
in 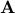 .
.
Lyapunov's sufficient condition for robust asymptotic stability: there exist  such that
such that
 is positive definite;
is positive definite;for every
 ,
,  is negative definite.
is negative definite.
The above is a semidefinite program, in matrix variable 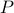 . (There is no objective function here; this is a feasibility problem.)
. (There is no objective function here; this is a feasibility problem.)
Robust linear control
What if a system is not stable? One way to stabilize it is via linear feeback, using this time an input that is a linear function of the state (which we assume is measured, hence available). That is, we set  where
where 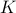 is a matrix of control parameters (or gains). The closed-loop system becomes
is a matrix of control parameters (or gains). The closed-loop system becomes

Applying the stability condition to the system above leads to a condition in  , that
, that

should be negative-definite for every  . The above matrix is not affine in the variables
. The above matrix is not affine in the variables  . However, the condition for a matrix
. However, the condition for a matrix 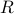 to be negative-definite is equivalent to the fact that
to be negative-definite is equivalent to the fact that  is, where
is, where 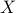 is an arbitrary invertible matrix. Applying this to
is an arbitrary invertible matrix. Applying this to  , and letting
, and letting  , we obtain that if there exist
, we obtain that if there exist  with
with 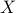 positive-definite, such that for every
positive-definite, such that for every  ,
,

is negative-definite, then the system can be stabilized by linear feedback.
In the case when the matrix ![[A(t),B(t)]](eqs/4221243930410602050-130.png) is not completely known, say it can take its values arbitrarily in a finite set
is not completely known, say it can take its values arbitrarily in a finite set ![mathbf{C} := { [A_1,B_1],ldots,[A_L,B_L]}](eqs/6780433875285304475-130.png) , then the condition: there exist
, then the condition: there exist  with
with 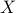 positive-definite, such that:
positive-definite, such that:

is negative definite, then the system is robustly stabilizable.